- 入驻时间: 2017-03-06
- 联系人:张婧
- 电话:0512-67089211
-
联系时,请说明易展网看到的
- Email:suz@tamasaki.com.cn
- Stucchi思多奇
- NITTO KOHKI日...
- Sankei
- KYOWA协和工业
- DIT东日技研
- AITEC艾泰克
- SIGMAKOKI西格玛...
- REVOX莱宝克斯
- CCS 希希爱视
- SIMCO思美高
- POLARI0N普拉瑞
- HOKUYO北阳电机
- SSD西西蒂
- EMIC 爱美克
- TOFCO东富科
- 打印机
- HORIBA崛场
- OTSUKA大冢电子
- MITAKA三鹰
- EYE岩崎
- KOSAKA小坂
- SAGADEN嵯峨电机
- TOKYO KEISO东...
- takikawa 日本泷...
- Yamato雅马拓
- sanko三高
- SEN特殊光源
- SENSEZ 静雄传感器
- marktec码科泰克
- KYOWA共和
- FUJICON富士
- SANKO山高
- Sugiyama杉山电机
- Osakavacuum大...
- YAMARI 山里三洋
- ACE大流量计
- KEM京都电子
- imao今尾
- AND艾安得
- EYELA东京理化
- ANRITSU安立计器
- JIKCO 吉高
- NiKon 尼康
- DNK科研
- Nordson诺信
- PISCO匹斯克
- NS精密科学
- NDK 日本电色
- 山里YAMARI
- SND日新
- Otsuka大塚电子
- kotohira琴平工业
- YAMABISHI山菱
- OMRON欧姆龙
- SAKURAI樱井
- UNILAM优尼光
- ONO SOKKI小野测...
- U-Technology...
- ITON伊藤
- chuhatsu中央发明...
OTSUKA大冢- 高分子相结构分析系统
 OTSUKA大冢- 高分子相结构分析系统ELSZ-2000SOTSUKA大冢- 高分子相结构分析系统ELSZ-2000SOTSUKA大冢- 高分子相结构分析系统ELSZ-2000S
OTSUKA大冢- 高分子相结构分析系统ELSZ-2000SOTSUKA大冢- 高分子相结构分析系统ELSZ-2000SOTSUKA大冢- 高分子相结构分析系统ELSZ-2000SOTSUKA大冢- 高分子相结构分析系统ELSZ-2000SOTSUKA大冢- 高分子相结构分析系统ELSZ-2000S
使用小角光散射法,能够实时解析高分子和薄膜的结构的装置。与使用X射线和中子线的装置相比,可以进行更大的结构(μm级)的评价。
从使用偏振片的Hv散射测量可以对光学各向异性的评价、结晶性薄膜的球晶直径的解析、Vv散射测量进行聚合物混合的相关长度的解析。
特长:
散射角度0.2~45°的测量可*短100msec测量。
评价亚微米~数100μm的结构。
也可以用专用的溶液池测量溶液样品。
在软件上轻松切换Hv散射和Vv散射测量。
台式实验室。
测量项目:
高的分子材料估价。
-结晶膜。
·结晶化温度、球晶径、结晶化速度。
·配光、光学各向异性。
-聚合物混合。
·相分离过程和相关长度(构造的大小)。
→高分子凝胶。
·三维架桥构造的大小。
-树脂。
·热硬化树脂和UV硬化树脂的硬化速度。
颗粒物性估价。
·粒子直径、凝集速度。
测量范围(理论值)。
球晶直径1.3~270μm。
粒子直径0.1~100μm。
相关长度0.1~100μm.
| 型式 | 高分子相構造解析システム |
| 測定原理 | 小角光散乱法 |
| 光源 | 半導体レーザ (波長785nm) |
| 検出器 | CMOSカメラ |
| 測定散乱角度 | 0.2°~45° |
| 取得像 | Hv光散乱像、Vv光散乱像 |
| 測定スポット | 約1mm |
| サンプルサイズ | *大10cm角 |
| ダイナミックレンジ | 120db以上 (HDR機能使用) |
| 測定時間 | 100ms~ |
| 解析項目 | 球晶径、相関長、粒子径など |
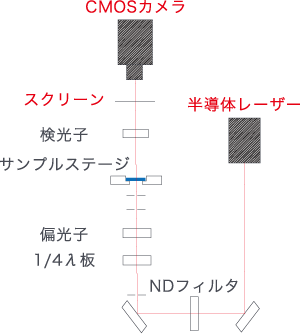
【手順】
1.サンプルステージにサンプルをセットします
2.検光子を測定したい対象に合わせて調整します。
3.サンプルからの散乱パターンがカメラに記録されます。
クロスニコル(偏光子と検光子が直交)で測定をします。
散乱体に光学異方性(複屈折)がある場合、散乱パターンが出現し、高分子の高次構造体のサイズ、秩序性、配向の評価が出来ます。
(測定例)結晶性フィルムの球晶径の解析
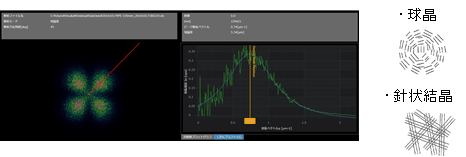
R = 4.09 / qmax
(R:球晶半径 、qmax:散乱光強度が*大になる散乱ベクトル )
散乱ベクトル q = 4π n/ λ sin( θ / 2 )
(λ:媒体中での波長、n:サンプル屈折率、θ:散乱角)
パラレルニコル(偏光子と検光子が平行)で測定します。
・ポリマーブレンドの相分離過程の評価
・海島構造の大きさ(相関長)
・粒子径の評価
(測定例) 相分離構造の相関長の解析
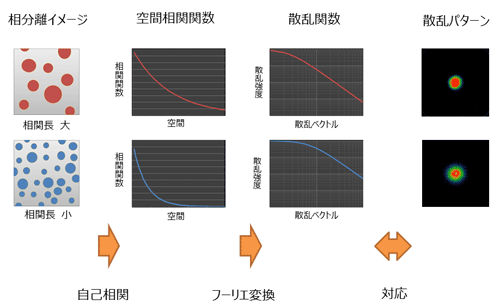
Debye-Bueche Plot
I(q) = A / (1+ξ2q2)2
(A:定数、ξ:相関長、q:散乱ベクトル)
ξ = √(a / b)
(ξ:相関長 、a:傾き、b:切片 )





