高光谱图像不仅包含空间信息,还包含丰富的光谱信息,目前已被广泛应用于农业、城市规划等领域。近年来,无人机的快速发展使高光谱在更多领域成为可能。无人机操控简单、成本相对较低、使用灵活,航空高光谱拍摄示意图如图1所示。但是航空高光谱技术也存在一些限制,当追求高的分辨率时,成像仪的视场角就会变小,从而导致成像区域变小。单幅图像很难覆盖大面积的区域,需要运用图像拼接技术得到一幅全景高光谱图像。

图1 航空高光谱拍摄示意图
普通图像的拼接领域已经获得了较多成果,但高光谱图像拼接的研究还并不是十分成熟。而且高光谱图像与普通图像存在一定的差异,高光谱图像的拼接目前面临了一系列的困难。高光谱图像有几十上百个波段,数据量非常大,直接对高光谱数据进行拼接会产生很大的计算量从而导致拼接时间过长,降低效率。其次,用于遥感的高光谱图像通常由机载设备拍摄,无人机拍摄的条件不稳定,飞机振动、曝光时飞机快速运动导致的像点偏移等现象会使拍摄得到的图像质量下降并且存在非刚性变换。这些情况造成特征点匹配时存在大量的误匹配。除此之外,无人机的飞行高度并不高,图像会存在视差,要得到好的高光谱拼接效果,需要解决上述挑战。在此背景下,迫切需要一种高精度的高光谱图像拼接方法。
武汉大学梅晓光副教授团队利用我司推扫式无人机高光谱成像系统(GaiaSky-mini)在300m高度拍摄的一组植物园场景。数据包含18 幅图像,大小为96×1057,光谱范围是400nm 到1000nm,共176 个波段。图2以伪彩色 图像的形式展示了18 张高光谱图像数据,选取的三个波段分别为第13 波段(436.5nm),第47 波段(547.6nm),第92 波段(700.2nm),将图片从左往右,从上往下依次标号为1-18。

图2 18幅高光谱图像数据
首先,选取一个波段作为参考波段,得到灰度图像后用SIFT算法提取相邻两幅图像的特征点。本研究对比了SIFT、SURF、SS-SIFT这三种特征点提取的算法。其中SIFT和SURF是针对单个波段的图像进行特征点的提取,SS-SIFT是针对高光谱的算法,所提取的特征点具有三维信息。实验选取图2中的第1、2作为图片进行测试,实验记录了三个算法的几个衡量指标,实验结果如表1所示。
表1 特征点提取的算法对比结果
|
特征点提取算法
|
提取特征点数量
|
匹配特征点数量
|
运行时间
|
|
SIFT
|
7455
|
1256
|
10.120s
|
|
SURF
|
467
|
80
|
0.849s
|
|
SS-SIFT
|
8304
|
82
|
950.311s
|
从以上实验结果可以看出,SS-SIFT相较于SIFT和SURF需要运行大量时间,降低了算法的效率,因此不能采用直接从高光谱图像数据中直接提取特征点的方法。SIFT和SURF算法相比较,SIFT的运行时间为10.012s,虽然没有SURF运行速度快,但是检测和匹配的特征点的数量足够多,使后续的图像配准更加准确。
无人机拍摄的遥感图像通常存在局部地形变化、尺度变化、旋转、视差以及其他非刚性变化等情况,在特征点的匹配过程中会造成很多误匹配现象。为了解决这个问题,本研究采用基于mTopKRP的算法来剔除误匹配,得到的结果如图3所示。
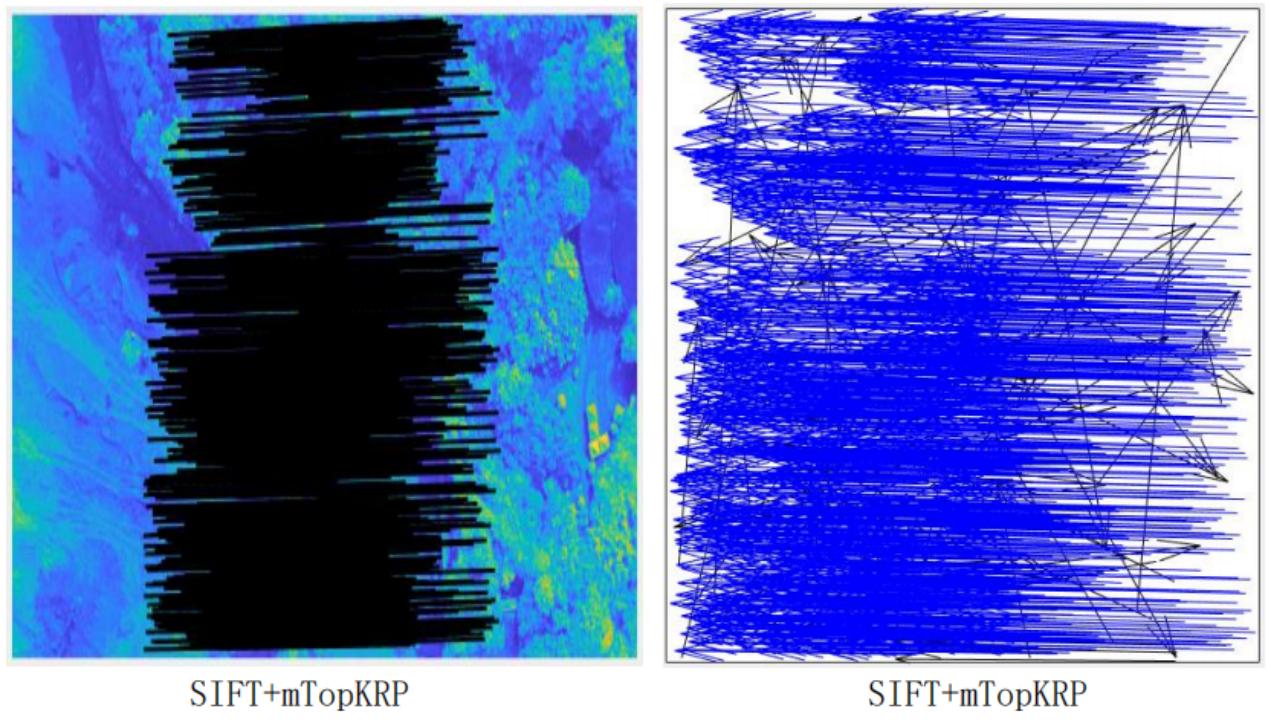
图3 通过mTopKRP算法剔除误匹配的结果
接下来,为了验证mTopKRP算法在剔除误匹配点上的优越性,我们对比了mTopKRP和其他误匹配剔除算法VFC和LPM。我们选择**率(precision),召回率(recall)和F-score作为评价特征点匹配算法的指标。得到的特征点匹配算法对比实验结果如图4所示。
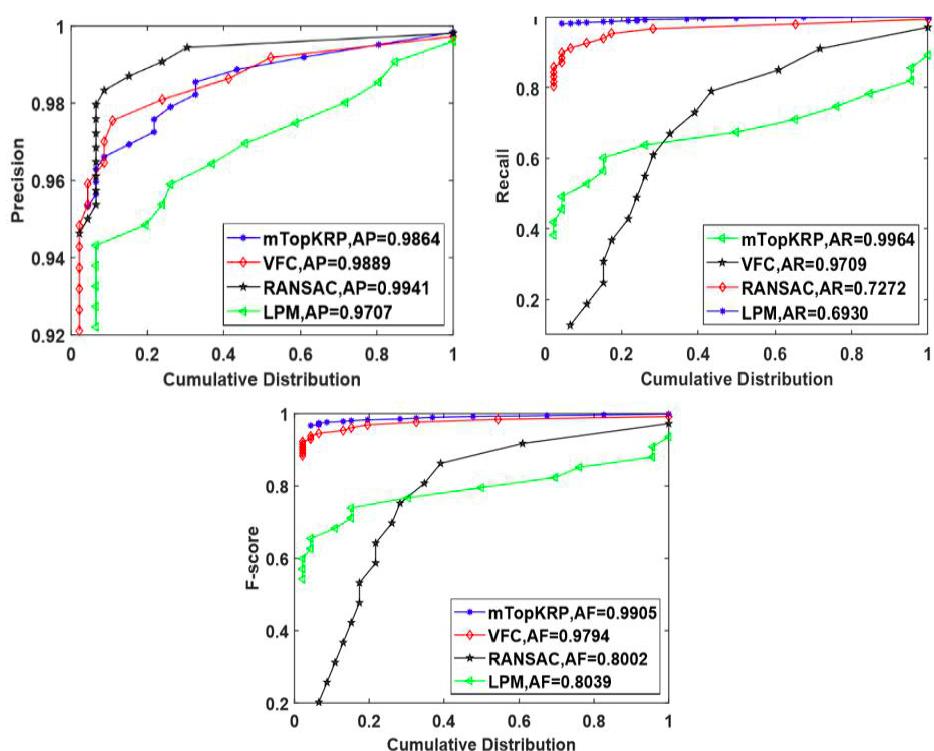
图4 特征点匹配算法对比实验结果
从以上实验结果中可以看出,无论是在图像存在刚性变换还是非刚性变换时,本研究特征点匹配算法mTopKRP都得到了更好的F-score,证实了我们的特征点匹配算法的优越性。在得到正确的匹配点集之后,我们需要用匹配的特征点来建立图片对之间的变换关系,即计算图片对之间的单应性矩阵。为了避免投影变换带来的失真,本研究采用基于鲁棒弹性扭曲的算法。并将本研究采用的图像变换模型和其他图像变换模型ANAP,NISwGSP和ELA进行对比,实验利用线性加权的图像融合算法,分别在单个波段拼接了18幅高光谱图像,得到图5的结果。

图5 图像拼接模型对比(从左到右ANAP、NISwGSP、ELA和本研究算法)
从实验结果中可以看出,算法ANAP,NISwGSP 和ELA 得到结果均在边处有明显的形变、不规则放大或扭曲。而本研究的鲁棒弹性变换模型更准确地对齐图像,在拼接后的非重叠区域消除了形变、扭曲等问题。本研究所采用的图像变换模型得到的拼接结果中图像清晰,没有明显模糊、重影的现象。
高光谱图像拼接的*后一步就是进行全波段的图像融合。将参考波段的鲁棒弹性变换模型参数运用于其他剩余波段,这样就可以获得所有波段的空间信息。在单个波段的重叠部分得到光谱值之后,将融合参数应用到其他波段,则全波段重叠部分都得到新的光谱值,非重叠部分的光谱值保留本身波段原有的光谱值。此处,将得到的高光谱全景图像用 RGB 图像的形式展示如图6所示。选取的三个波段分别为第 13 波段 (436.5nm),第 47 波段(547.6nm),第 92 波段(700.2nm)。

图6 以RGB形式展示的高光谱图像整体拼接结果
对于图像的光谱进行分析可以实现对地物的分类和识别,所以拼接任务除了关注空间信息外,还应对光谱曲线进行分析。理想情况下拼接后的全景图在重叠区域的光谱曲线应该与参考图像的保持一致。通过计算两个光谱曲线的光谱角大小(SAD),可以判断它们的相似程度。找出在图1、2重叠部分的两对典型地物(土地和植被),分别记录为A、A′ 和B、B′,如图7所示。由于图像1是参考图像,因此拼接得到的高光谱图像的光谱曲线应该与图像1的光谱曲线接近。通过图8计算得到,对于同名点对A、A′,图像1和2在此点的光谱角为0.0894。在同名点B、B′,图1与图2 光谱角大小为0.0471。因此,可以得出结论,在原始图像同名点对的光谱值有较大差异的情况下,本研究的算法得到的图像的光谱接近于参考图像,保证了光谱信息的一致性。

图7 同名点对示意图

图8 光谱分析曲线
本研究提出了新的高光谱图像拼接方法,适用于存在旋转、尺度变化、非刚性变换的图像集。得到的图像清晰,无明显错误拼接和接缝,图像的光谱曲线失真较小,适用于存在大视差的机载高光谱图像。
通讯作者简介:
梅晓光,博士,武汉大学电子信息学院副教授,博士生导师。
主要研究方向:高/超光谱应用中的计算机视觉、机器学习等相关问题的研究。
参考文献:Yujie Zhang, Zhiying Wan, Xingyu Jiang and Xiaoguang Mei, in IEEE Journal of Selected Topics in Applied Earth Observations and Remote Sensing, vol. 13, pp. 3145-3154, 2020, doi: 10.1109/JSTARS.2020. 3001022.
