红外光谱分析技术由被测样品的红外光谱主导,由红外光谱仪得到的光谱信号中不仅含有样品的信息,还包含了噪声和各种外界干扰因素。为了使定量分析模型更加稳健和**,需对光谱进行去噪预处理。
平均平滑法
根据红外光谱图中的吸收峰是否消失或采用偏*小二乘法(PLS)建模后得出的均方根误差(RMSE)确定出预处理方法的*佳参数。平均平滑的数据点数通常从20以内的奇数中选择,平滑的点数越高,光谱越平滑,去噪效果越好,但所得光谱的分辨率越低,光谱的有些肩峰会消失。考察范围为从5点开始,间隔为2点,分别进行平滑,结果如图3~7所示。当平滑点数为11点时,波数为967处的肩峰开始消失,当平滑点数为13点时,波数为967处的肩峰完全消失,因而样品的平均平滑点数选择9点
图3.5点平均平滑
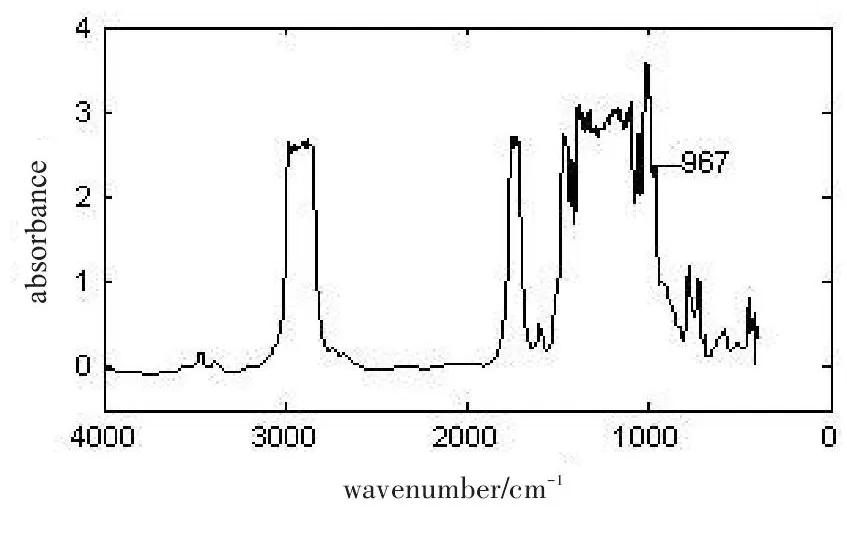
图4.7点平均平滑
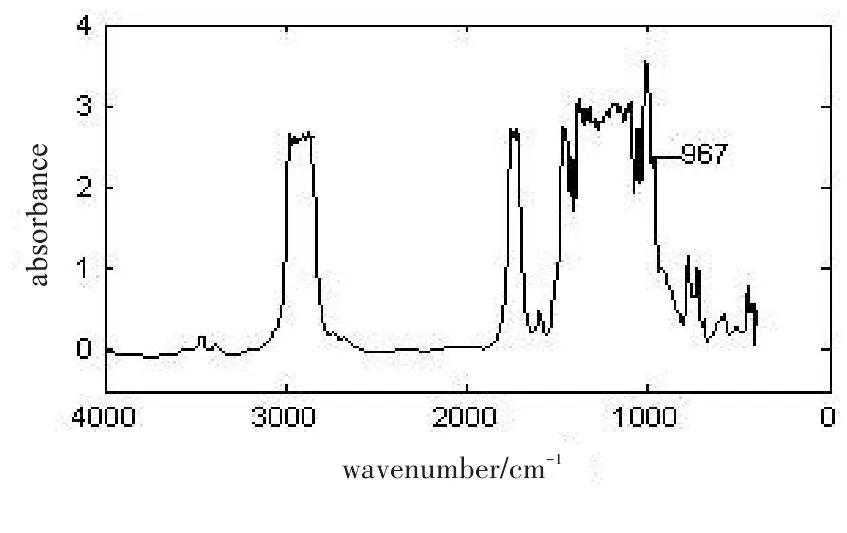
图5.9点平均平滑
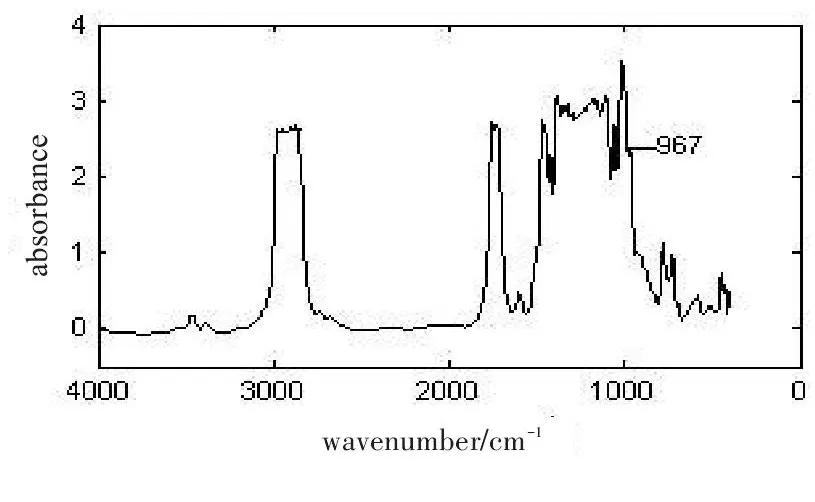
图6.11点平均平滑
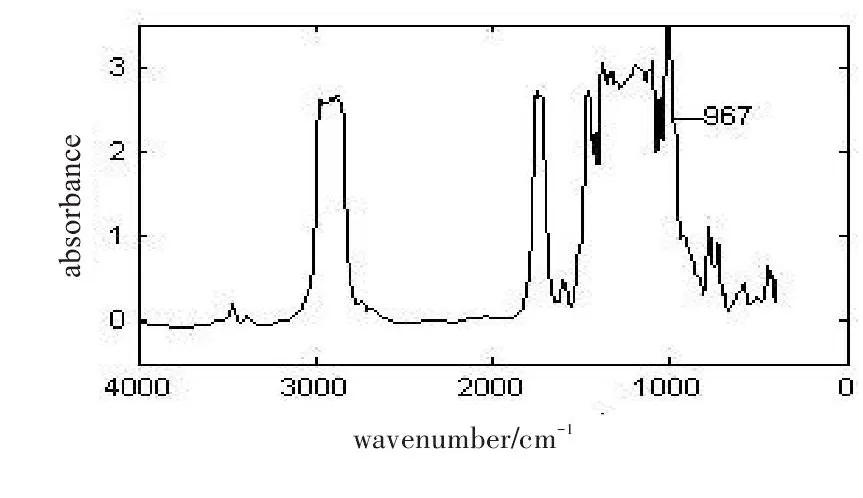
图7.13点平均平滑
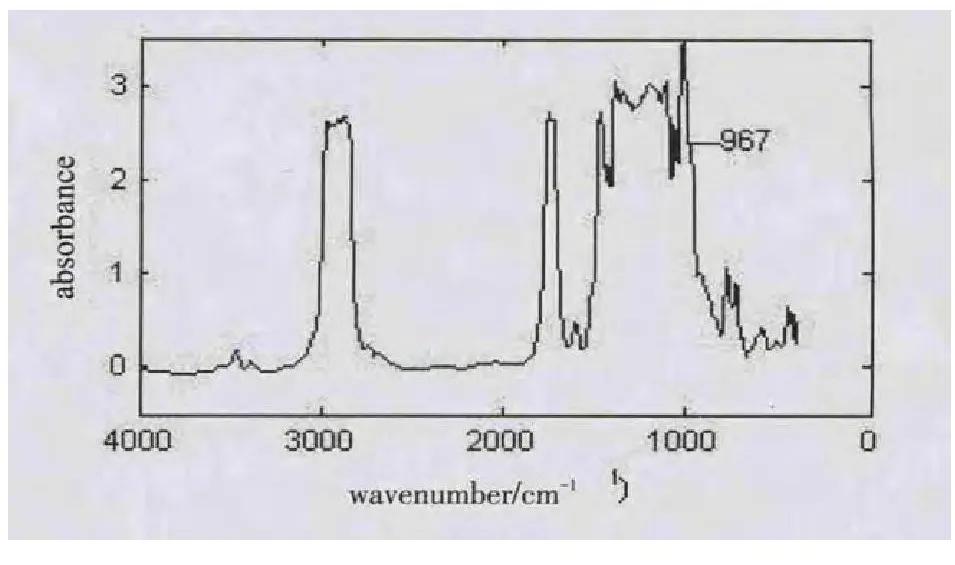
Savitzky-Golay平滑法
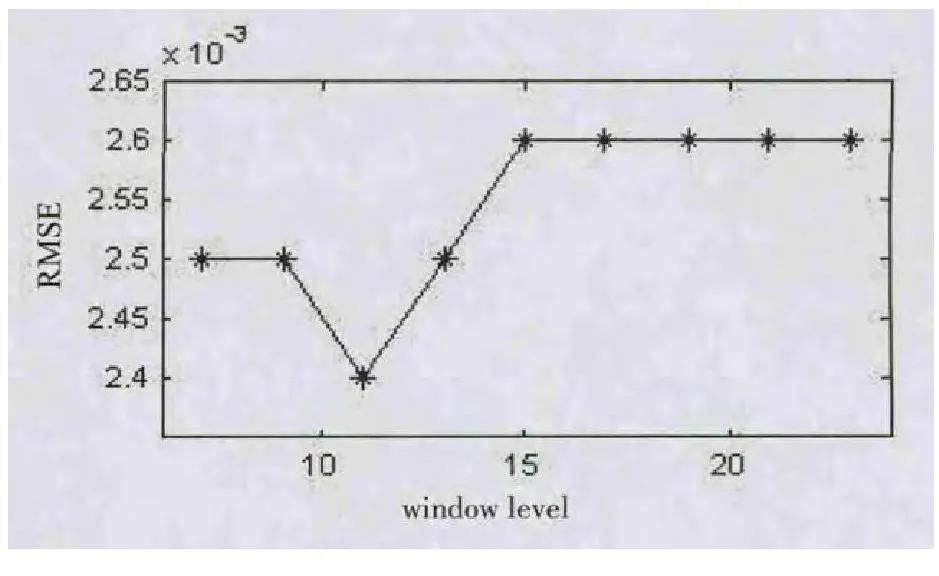
Savitzky-Golay卷积平滑法是1964年Savitzky和Golay提出并**运用于信号滤波处理的平滑方法,该方法与移动平均平滑法的基本思想是类似的,只是没有进行简单的平均,而是通过多项式来对移动窗口内的数据进行多项式*小二乘拟合,其本质是一种加权平均法,强调中心点的中心作用。采用SavitzkyGolay平滑,平滑的窗宽值是一个重要参数。如果窗宽值选择较小,平滑去噪效果不好;如果窗宽值选择较大,则会造成光谱信号失真。因此,要选择合适的窗宽值,考察范围为7~23,间隔为2,在选择不同的窗宽值后发现红外光谱图的特征峰均还存在,因而需要用偏*小二乘法对不同的窗宽值的平滑结果建立模型后比较均方根误差(RMSE)的值来确定出*佳的窗宽值,结果如图8所示。当窗宽值为11时,均方根误差(RMSE)*小,所以样品的Savitzky-Golay平滑窗宽值选择11。
图8.Savitzky-Golay平滑窗宽值的选择
小波包变换预处理
小波包变换是基于小波变换的进一步发展,能够提供比小波变换更高的分辨率。小波包分解与小波分解相比,是一种更精细的分解方法。
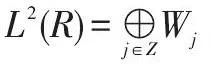
在多分辨分析中,表明多分辨分析是按照不同的尺度因子j把Hilbert空间L2(R)分解为所有子空间Wj(j∈Z)的正交和,其中,Wj为小波函数φ(t)的闭包(小波子空间)。
小波包分析就是进一步对小波子空间Wj按照二进制分式进行频率的细分,以达到提高频率分辨率的目的。
小波包降噪的步骤
小波包分析的一般步骤如下。
1)信号的小波包分解。选择一个小波并确定小波分解的层次N,然后对信号进行小波包分解。
2)确定*优小波包基。对于一个给定的熵标准,计算*优树。
3)小波包分解系数的阈值量化。对于每一个小波包分解系数,选择一个恰当的阈值并对系数进行阈值量化。
4)信号的小波包重构。根据*底层的小波包分解系数和经过量化处理的系数进行小波包重构。
小波包变换参数选择
小波包变换对红外光谱图进行去噪处理,采用了软阈值和“db3”小波包基。但信号尺度的分解层数是影响去噪效果的一个重要因素,一般情况下分解层数较少,去噪效果不理想;但分解层数较多,导致运算量增大,且会造成信息的丢失。
通常分解层数在3层或3层以上,所以选择从考察3层开始考察,分别进行小波包变换去噪,结果如图9~11所示。在分解层数为4层时,波数为1422处的吸收峰已经基本消失,在分解层数为5层时,波数为1422处的吸收峰已经完全消失,所以信号尺度的分解层数选择3层。
图9.分解层数为3层的小波包变换
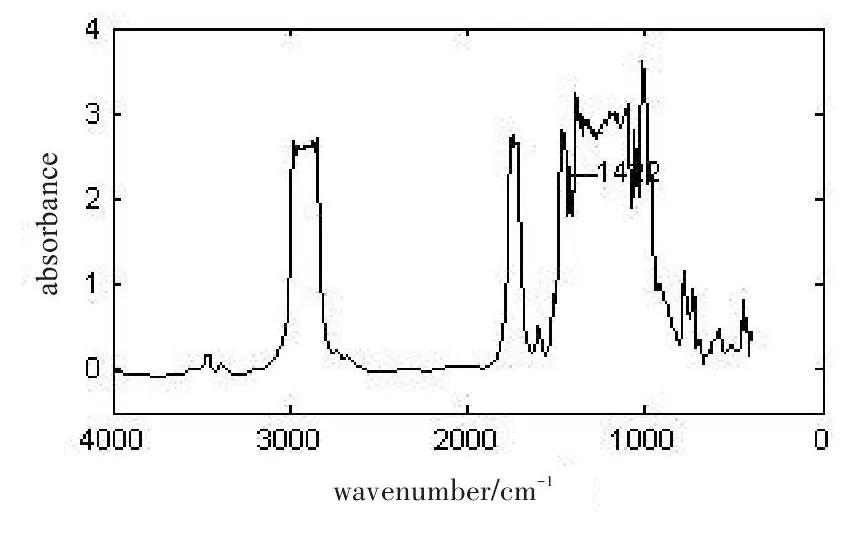
图10.分解层数为4层的小波包变换
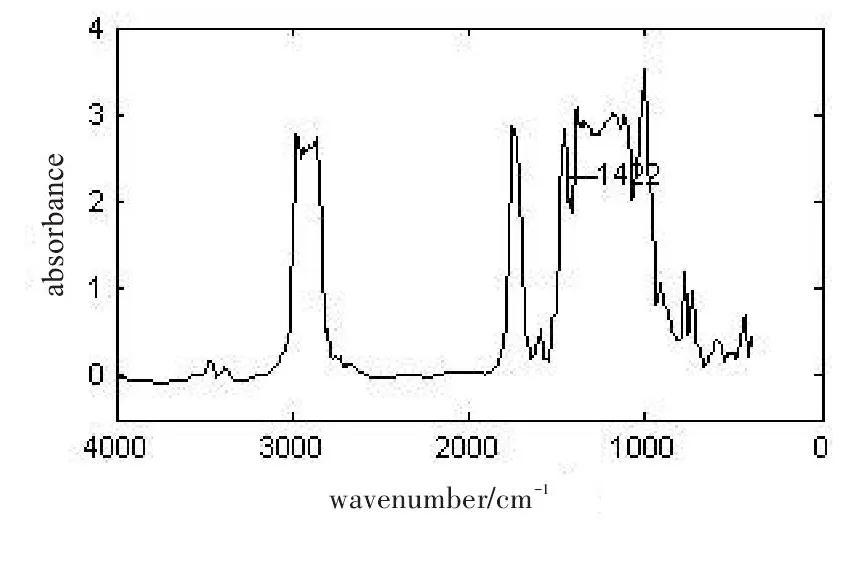
图11.分解层数为5层的小波包变换
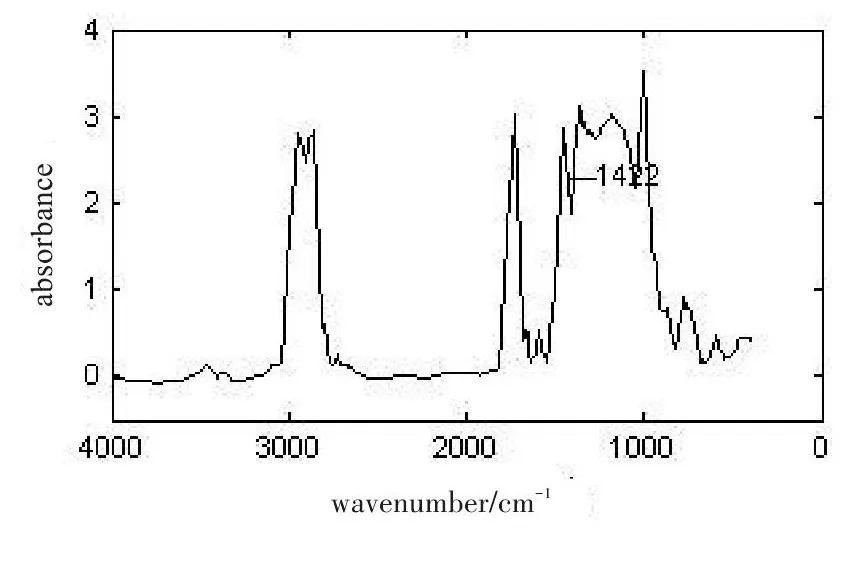
通过上述3种方法分别对获得的红外光谱进行预处理,再采用偏*小二乘法(PLS)对这3种预处理后的红外光谱进行总酸值建模预测,并以相对误差值(RE)作为评价标准,结果如图12和表1所示。图12中,“○”线、“□”线、“+”线分别是是平均平滑法(9点)、Savitzky-Golay平滑法(窗宽值11)和小波包变换预处理后建模的预测相对误差。
图12.3种预处理方法建模结果的对比
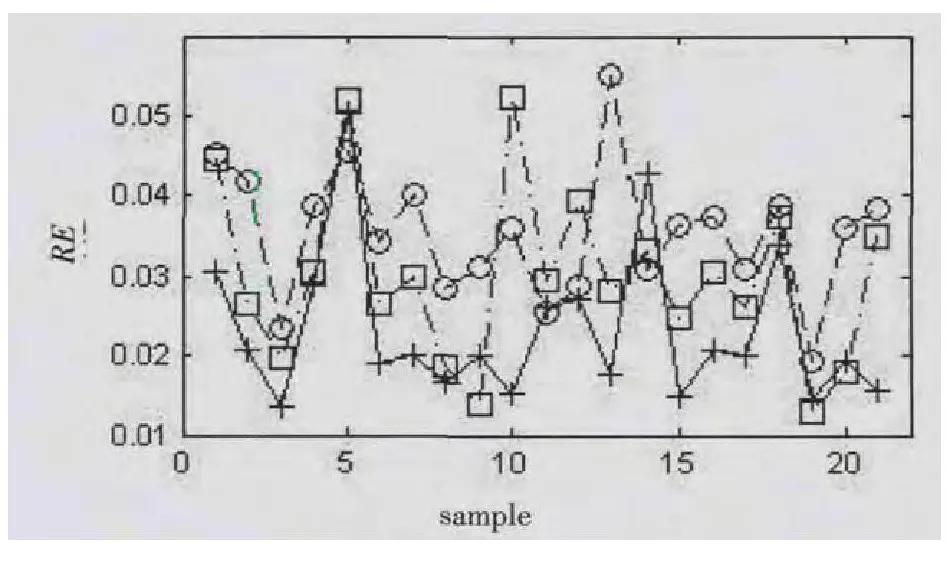
表1.不同预处理后的预测结果
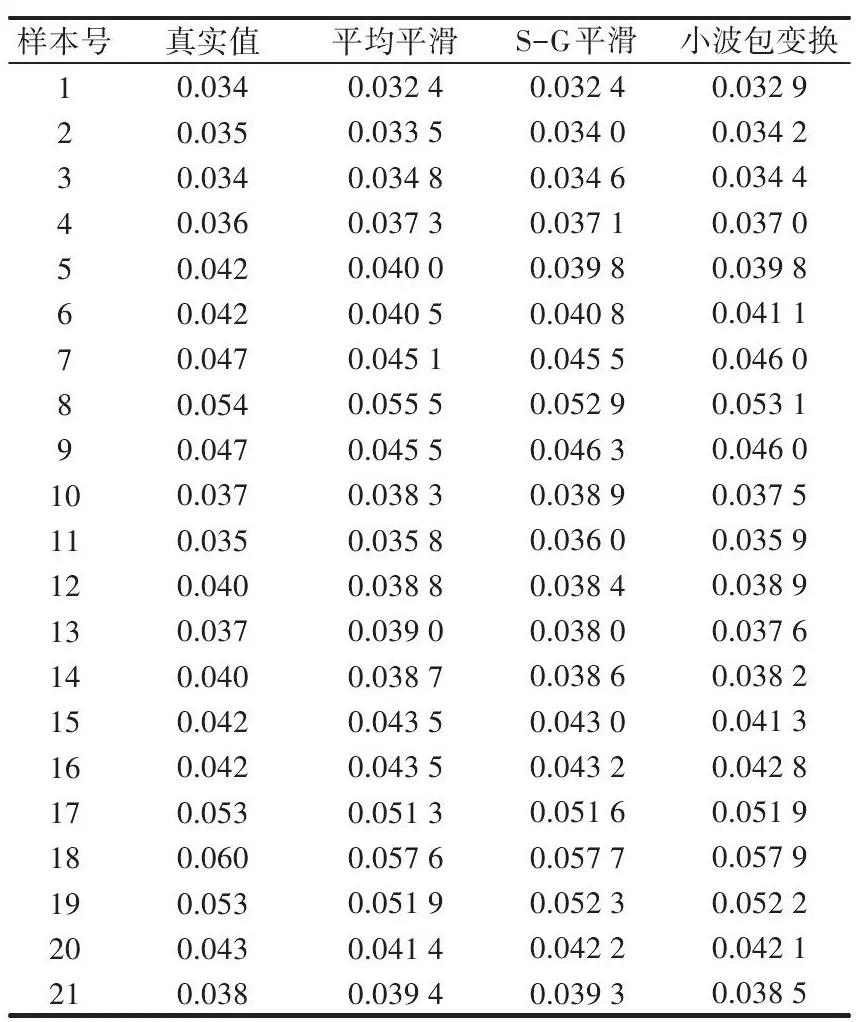
样本的预测相对误差分布在1.1%~5.5%之间,大部分样本在利用小波包变换进行红外光谱去噪预处理后建模的相对误差较其余两种平滑去噪方法小,样本的相对误差超过4.0%的有2个,大部分建模样本的相对误差在3.0%以内,符合模型预测要求。